今天給大家帶來(lái)的是行測數學(xué)運算解題技巧梳理的第五期，也是最后一期了。本期主要介紹如何利用數字特性法排除無(wú)關(guān)的選項，甚至能幫我們直接選出答案的。詳情如下：
看過(guò)了解題方法，我們還是先通過(guò)一道真題來(lái)看一下——
【經(jīng)典真題】
兩箱同樣多的蛋黃派分別分發(fā)給兩隊志愿者做早餐，分給甲隊每人6塊缺8塊，分給乙隊每人7塊剩6塊，已知甲隊比乙隊多6人，則一箱蛋黃派有（）塊。
A.120 B.160 C.180 D.240
【解析】正確答案為B。此題很簡(jiǎn)單，只要利用數字特性法能直接幫我們排除不正確的選項，具體如何操作呢，來(lái)看老師分析。
以上視頻截取自國考系統班，更多視頻解析查看鏈接：http://www.chinaexam.org/course/list?tag=2。
聽(tīng)完了老師講解，是不是覺(jué)得茅塞頓開(kāi)了呢，大家一鼓作氣，再通過(guò)3道真題來(lái)練練手吧。
【例1】（2018年國考省級以上試卷第75題）一輛汽車(chē)第一天行駛了5個(gè)小時(shí)，第二天行駛了600公里，第三天比第一天少行駛200公里，三天共行駛了18個(gè)小時(shí)。已知第一天的平均速度與三天全程的平均速度相同，則三天共行駛了多少公里（）。
A．800 B．900 C．1000 D．1100
【解析】正確答案為B。
本題利用數字特性法，因全程的時(shí)間為 18 小時(shí)，故路程應為 18 的倍數，四個(gè)選項中只有 900 符合。因此 B 項當選。
【例2】（2017年國考副省級級試卷第62題）某人出生于20世紀70年代，某年他發(fā)現從當年起連續10年自己的年齡與當年年份數字之和相等（出生當年算0歲）。問(wèn)他在以下哪一年時(shí)，年齡為9的整數倍（）。
A．2006年 B．2007年 C．2008年 D．2009年
【解析】正確答案為B。
方法一：設出生年份為1970+x年。若當年為1980+A年，根據連續10年自己的年齡均與當年年份數字之和相等，可得：(1980+A)-(1970+x)=1+9+8+A，解得x=-8，不滿(mǎn)足條件；若當年為1990+B年，可得：(1990+B)-(1970+x)=1+9+9+B，解得x=1，即出生于1971年，依次代入選項：2006年為35歲，不符合9的整數倍，排除A；2007年為36歲，是9的整數倍，符合題意。故正確答案為B。
方法二：若1980年，數字之和為1+9+8+0=18，若滿(mǎn)足年齡等于當年年份數字之和，則出生年份=1980-18=1962，不滿(mǎn)足出生于20世紀70年代；若1990年，數字之和為1+9+9+0=19歲，若滿(mǎn)足年齡等于當年年份數字之和，則出生年份=1990-19=1971，滿(mǎn)足出生于20世紀70年代，且從1990年開(kāi)始連續十年都滿(mǎn)足要求。所以出生年份為1971年，依次代入選項2006年為35歲，不符合9的整數倍，排除A；2007年為36歲，是9的整數倍。符合題意。
【例3】（2018年浙江A類(lèi)第64題）小王購買(mǎi)甲、乙兩種特價(jià)商品。甲商品打八折后每件52元，乙商品打八五折后每件34元，小王購買(mǎi)這些商品總共比打折前節省了83元。問(wèn)他購買(mǎi)這兩種特價(jià)商品總共支出了多少元？
A.544 B.445 C.427 D.362
【解析】正確答案為D。
根據甲商品打八折后每件52元，可計算出甲的售價(jià)為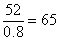
元；根據乙商品打八五折后每件34元，可計算出乙的售價(jià)為
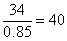元。甲商品一件節省65-52=13元，乙商品一件節省40-34=6元。設購買(mǎi)甲商品x件，乙商品y件，由于小王購買(mǎi)這些商品比打折前節省了83元，可得13x+6y=83，該式為不定方程，結合奇偶特性，可得x=5，y=3，即甲、乙兩種商品分別買(mǎi)了5件、3件。購買(mǎi)這兩種特價(jià)商品總支出為：52×5+34×3=362元。
以上是行測數學(xué)運算解題技巧梳理第五期內容，至此數學(xué)運算解題技巧已梳理完結。下周開(kāi)始我們會(huì )有全新的內容，敬請期待。
往期閱讀：
